飛んでいる矢は本当に止まっているのか?ゼノンのパラドックスから考える時間と空間の謎とは!?
💡 ゼノンのパラドックスは、古代ギリシャの哲学者ゼノンが提唱した、時間と空間に関する逆説です。
💡 代表的なパラドックスとして、アキレスと亀のパラドックスや、飛んでいる矢のパラドックスがあります。
💡 これらのパラドックスは、一見矛盾する論理によって、私たちが当たり前と思っている時間や空間の概念を揺さぶります。
それでは、最初のテーマに移りましょう。
飛んでいる矢のパラドックス:瞬間の謎
飛んでいる矢のパラドックスは、まさに時間と空間の概念を根底から覆すような問題提起ですね。
公開日:2023/06/25

✅ ゼノンのパラドックスの一つである「アキレスと亀」は、アキレスが亀に追いつくには、二人の間の距離を無限に分割しなければならないため、永遠に追いつけないというものです。これは無限分割の罠であり、実際には有限の時間で追いつくことが可能です。
✅ 「飛ぶ矢は静止しているので飛ばない」というパラドックスは、瞬間が存在するのかという疑問を投げかけます。しかし、この宇宙には時間間隔がゼロになる瞬間は存在せず、すべての物理量は揺らいでいるため、矢は止まっているのではなく、有限の時間幅の中で動いていると考えるべきです。
✅ ゼノンのパラドックスは、無限分割や瞬間の存在といった、私たちが当たり前に思っている概念を疑うことで、時間や空間の概念について深く考えさせてくれます。これらのパラドックスは、科学や哲学において重要な議論の題材となっています。
さらに読む ⇒Smart FLASH/スマフラ光文社週刊誌 - 今を撃つ、政治・経済・社会・芸能・スポーツなど幅広い企画力と、読み応えのある大特集記事で、ビジネスマンを中心に支持されているビジュアル総合週刊誌です!出典/画像元: https://smart-flash.jp/lifemoney/241227/1/1/なるほど、瞬間の概念を深く考えさせられる内容ですね。
古代ギリシャの哲学者ゼノンが提唱した「飛んでいる矢のパラドックス」は、飛んでいる矢は瞬間を切り取れば止まっている状態であり、その瞬間の積み重ねで時間を作っても、矢は動いていないという主張です。
このパラドックスは、瞬間を0と捉えることで、数学的に誤った計算をしてしまっていることが原因です。
実際には、瞬間は0ではなく、限りなく0に近い時間であるため、微分のように微小な時間tを用いて計算することで、飛んでいる矢は止まっていないことが証明できます。
このパラドックスを通して、時間や運動を理解する上で「0に近づける」と「0に等しい」という違いが重要であることを学びました。
うむ、深いな。哲学ってやっぱり奥深いんやね!
ゼノンのパラドックス:アキレスと亀、そして飛んでいる矢
アキレスと亀のパラドックスは、一見するとアキレスは永遠に亀に追いつけないように思えますが、実際にはそうではないんですよね。
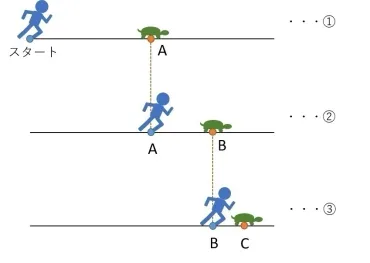
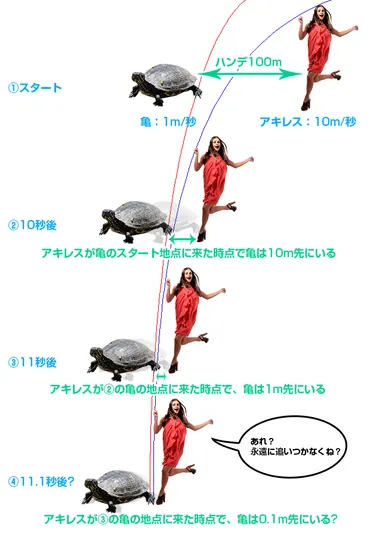
✅ アキレスと亀のパラドックスは、古代ギリシャの哲学者ゼノンが提示したもので、速いアキレスが遅い亀に追いつけないという一見矛盾する論理です。
✅ ゼノンの論理では、アキレスが亀に追いつくためには、まず亀がいた場所まで到達しなければならず、その間に亀は少し先に進みます。このプロセスを繰り返すと、アキレスは常に亀より少し遅れてしまい、永遠に追いつけないとされます。
✅ このパラドックスは、時間と空間が無限に分裂できるという前提に基づいており、実際には時間と空間は有限であり、アキレスは有限時間で亀に追いつくことができるという現実との矛盾から生じています。
さらに読む ⇒Yahoo!ニュース出典/画像元: https://news.yahoo.co.jp/articles/ed6037c09f7deddb9a90eef196936af853d36a2a?page=2確かに、無限分割という考え方は、私たちの直感に反する部分がありますね。
ゼノンのパラドックスは、運動や空間に関する逆説であり、有名な例として、アキレスと亀のパラドックスや飛んでいる矢のパラドックスがあります。
アキレスと亀のパラドックスは、アキレスが亀に追いつくまでに、亀は常に少し先へ進むため、アキレスは永遠に亀に追いつけないというものです。
これは、無限に分割できる空間を前提として、無限回の移動が必要になるという論理に基づいています。
しかし、実際には有限の時間でアキレスは亀に追いつきます。
飛んでいる矢のパラドックスは、矢は常に特定の瞬間に止まっているため、動いていないという主張です。
これは、瞬間を無限に分割できるという考え方から生まれます。
しかし、現代の物理学では、瞬間は無限に分割できるのではなく、極めて短い時間として定義され、この時間の間に矢は速度を持って移動しています。
昔の人は、こんな難しいことを考えてたんですね。すごいわ!
無限と有限の狭間:ゼノンのパラドックスの深淵
ゼノンのパラドックスは、無限という概念を扱う上で、非常に重要な問題提起だと思います。
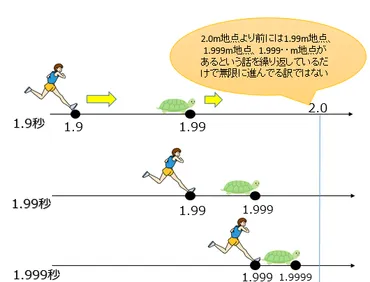
✅ 「アキレスと亀」は、アキレスがどれだけ速く走っても、亀に追いつけないというゼノンのパラドックスです。これは無限に続く距離を仮定することで、追いつけないという結論を導き出しています。
✅ しかし、実際にはアキレスは有限時間で亀に追いつきます。パラドックスは、距離を無限に分割することで時間についても無限に分割してしまうという誤った考え方から生まれました。
✅ ゼノンは、このパラドックスを通して、無限という概念が当時のピタゴラス学派の主張と矛盾することを示そうとしていました。
さらに読む ⇒アタリマエ!|当たり前だけどアタリマエじゃない事を、アタリマエにする出典/画像元: https://atarimae.biz/archives/5584無限と有限の関係は、人間の思考にとって永遠の課題なのかもしれません。
ゼノンのパラドックスは、無限の概念と有限の概念の矛盾を示すものであり、数学や物理学の発展に大きな影響を与えました。
これらのパラドックスは、空間や時間の概念、運動の定義などを再考するきっかけとなり、現代における微分積分などの概念誕生につながりました。
アキレスと亀のパラドックスは、アキレスが亀に追いつくためには、直前に亀がいた位置に到達する無限回の行為の試行が必要であり、それは、ゴールに到達するまでに無限数の点を通過することが必要な、二分法のパラドックスと同じ議論であることを明らかにしました。
現実の世界では、アキレスは亀に追いつきますが、ゼノンのパラドックスの世界では、永遠に追いつけないという結論が生じています。
無限って、ほんまに存在するんかな?
数学的証明:アキレスは追いつくのか?
実際に検証するとなると、なかなか難しい問題ですね。
✅ この記事は、ゼノンのパラドックスの中でも有名な「アキレスと亀」のパラドックスについて、分かりやすく説明しています。
✅ 記事では、亀と人間が競走したら、亀が絶対に勝つという結論を導き出すパラドックスを、実際に検証するために、亀の代わりに亀の格好をした人が登場します。
✅ しかし、本物の亀を手に入れることが難しく、かつ、企画終了後に亀の面倒を見る責任が生じることから、最終的には亀の格好をした人が実際に走るという、現実的な検証方法に変更されました。
さらに読む ⇒バケモノ.jp出典/画像元: http://bakemono.jp/special/monthly/1962/数学的に証明することで、パラドックスの謎が解き明かされていくんですね。
このパラドックスを解決するために、アキレスが亀に実際に何秒後に追いつくのかを数学的に計算すると、アキレスは11.11111…秒後に亀に追いつくことがわかります。
さらには、アキレスが亀に追いつくまでの時間を、直前の亀の位置にたどり着くのにかかる時間の総和として捉えた場合、その総和を無限級数で表すことができます。
この無限級数の和も、11.11111…となり、数学的にアキレスは亀に追いつくことが証明されます。
しかし、ゼノンの議論と数学的な議論は、相反する結論を生み出しています。
次回はこの相反する二つの論理の関係性について考えていきます。
なるほど、数学的に証明すればアキレスは追いつくってことか。
ゼノンのパラドックス:時間と空間の連続性
ゼノンのパラドックスは、時間と空間に関する深い洞察を与えてくれますね。
公開日:2023/10/06

✅ ゼノンのパラドックス「飛ぶ矢は飛ばない」は、時間の一点を切り取れば矢は常に静止しており、止まっている状態をいくら集めても運動にならないため、飛ぶ矢は飛ばないと主張する。
✅ アリストテレスは、ゼノンの主張は時間の一点だけを見ており、静止または運動状態を判断するには時間に幅が必要であるため誤りだと反論する。
✅ 数学的に考えると、速度は距離を時間で割ることで求まるが、時間が流れない場合、ゼロで割ることになり、速度を求めることができないため、ゼノンの主張は誤りとなる。
さらに読む ⇒遊ろじー出典/画像元: https://penseur.blog/paradox-of-zeno/時間の一点だけを見るのではなく、時間の幅を考慮することが重要であるということがよく分かります。
ゼノンのパラドックスは、古代ギリシャの哲学者ゼノンが提唱した「飛ぶ矢は飛ばない」という逆説です。
彼は、矢が飛んでいる間、時間の一点を切り取れば矢は必ず静止しているため、運動は静止の集積にすぎず、矢は飛んでいないと主張しました。
しかし、アリストテレスはゼノンの主張は誤りだと反論しました。
彼は、静止と運動は時間の中での位置の変化によって定義され、時間の一点のみを捉えることで静止と運動を区別することはできないと指摘しました。
また、数学的に考えても、時間が流れない場合、速度を求める式は成立せず、ゼノンの主張は成り立たないと説明しました。
ゼノンのパラドックスは、時間と空間の連続性を示す問題提起であり、哲学や物理学において重要な論点となっています。
ゼノンのパラドックス「矢(飛ぶ矢)」は、矢がそれぞれの瞬間に静止しているため運動していないと主張するものです。
このパラドックスを解くには、「運動」を「データ」として捉える必要があります。
これは、運動は主観的な観測であり、「動いている物体」そのものではないということです。
つまり、矢が静止しているように見えるのは、運動のデータとしての位置を、勘違いされた客観的な運動の連続上の点と比較しているためです。
客観的には、動いている物体は、客観的な位置の移動による「糸」を引いていない状態で存在しており、軌跡は主観的な作業によるものです。
あら、時間って奥が深いですね。
ゼノンのパラドックスは、時間と空間の概念について、私たちに深い思考を促してくれるものですね。
💡 ゼノンのパラドックスは、時間と空間を無限に分割できるという前提から生まれたものであり、実際には時間と空間は有限であるということが分かります。
💡 アキレスと亀のパラドックスは、アキレスが亀に追いつくためには、無限回の移動が必要になるという論理に基づいています。
💡 飛んでいる矢のパラドックスは、矢は常に特定の瞬間に止まっているため、動いていないという主張ですが、実際には矢は有限の時間幅の中で動いています。