波数の世界へようこそ!波数とエネルギーの関係を徹底解説(?マーク)波数、波長、振動数、エネルギーの関係を分かりやすく解説!
波数の基本を徹底解説!単位換算をマスターして、分光法や電磁波解析を理解しよう。カイザー(cm⁻¹)とnm、m⁻¹の変換、さらには波数とエネルギーの関係を、具体的な計算例を通して分かりやすく解説。技術文書の解析に役立つ、波長、波数、周波数の相互変換の秘訣がここに!
単位変換:実用的な計算方法
波数と波長、nmとcm-1、簡単に変換する方法は?
逆数取り、10の7乗をかける!
この章では、単位変換に焦点を当て、実用的な計算方法を解説します。
cm-1とnmの変換など、具体的なケーススタディを通して理解を深めましょう。
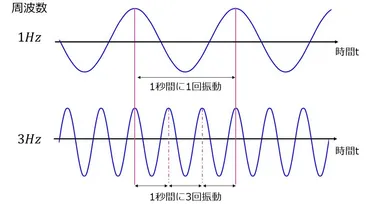
✅ 波長と周波数の相互変換を行うツールであり、波長から周波数と周期へ、または周波数から波長と周期への変換ができる。
✅ ツールの使い方は、単位を選択し、波の種類を選ぶことで波の速度が自動入力される。出力の小数点以下の桁数や表示形式(指数表示/小数表示)も設定可能。
✅ 波長、周波数、周期の計算式が解説されており、波の速度、波長、周波数の関係式を用いて変換を行う。光の波長を周波数に変換する場合は、光速を使用する。
さらに読む ⇒光学技術の基礎用語出典/画像元: https://www.optics-words.com/kogaku_kiso/wave_calculation.html単位変換は、技術文書を読む際にも必須の知識ですよね。
cm-1とnmの変換は、特に覚えておくと便利ですね。
計算例も分かりやすかったです!。
技術文書の解析などでは、様々な単位間の変換が不可欠です。
cm-1とnmの変換は重要であり、Xcm-1=(1/X)cm=(1/X)×10^7nm、Ynm=Y×10^-7cm=(1/Y)×10^7cm-1の関係が成り立ちます。
また、cm-1とm-1の変換は、1cm-1=100m-1、1m-1=0.01cm-1となります。
例えば、波長400nmの光の波数は2.5×10^12 m-1となります。
これらの変換は、各単位の前の数値の逆数を取り、10の7乗をかけることで実現できます。
計算例として、波数overline{u}=2×10^4cm^{-1}における波長λと周波数uの計算が可能です。
計算時には、桁数の変化に注意することが重要です。
あらまあ!単位変換ですって?そんなの、ワシには朝飯前じゃよ!昔はね、もっと複雑な計算をしてたんじゃよ!単位なんてものは、所詮記号じゃからね!
波数とエネルギーの相互変換:具体例
エネルギーと波数の関係は?換算の計算方法とは?
E=hc/λ。波数を用いてE = hc × 波数。
最後の章では、波数とエネルギーの相互変換について、具体的な計算問題を通して理解を深めます。
実践的な問題を通じて、知識を定着させましょう。

✅ 光子のもつエネルギーを求める問題で、アインシュタインの光量子仮説と光の波長の関係を利用する。
✅ 光子のエネルギーEは、E=hνで求められ、振動数νが不明な場合は、(光速c)=(振動数ν)×(波長λ)の関係からνを求め代入する。
✅ エネルギーをJからeVに変換するには、1eV=eJの関係を用いて、エネルギーEJを電荷eで割り算する。
さらに読む ⇒勉強のわからないを5分で解決出典/画像元: https://www.try-it.jp/chapters-8806/sections-8807/lessons-8808/practice-3/具体的な計算例を通して、波数とエネルギーの相互変換を理解できるのは良いですね。
公式を覚えるだけでなく、実際に問題を解くことで、より深く理解できます。
波数とエネルギーの変換方法について、具体的な計算問題を通して理解を深めます。
エネルギーEは波長λを用いてE=hc/λで表され、これを波数に変換することで、エネルギーと波数の換算式が導出されます(E = hc × 波数)。
例題1として、波数が50cm-1の光のエネルギーを求めると、9.9 × 10^-22 Jとなります。
例題2では、エネルギーが5 × 10^-20 Jの光の波数を求めると、2525cm-1となります。
このような計算を通して、波数とエネルギーの相互変換の理解を深めることができます。
えー、計算問題とかマジ勘弁!でも、波数からエネルギーが求められるってことは、なんかスゴイってことは分かった!
本日は、波数に関する基礎知識から応用まで、幅広く解説しました。
皆様の理解の一助となれば幸いです。
💡 波数とは何か?基本概念と単位について理解を深めました。
💡 波長、振動数、エネルギーの関係を学び、相互変換の計算方法を理解しました。
💡 単位変換の具体的な計算方法を学び、実用的な知識を習得しました。