固体物理学入門：電子とエネルギーバンド構造の世界？電子の振る舞いを理解するための基礎知識：Blochの定理とエネルギーバンド

それでは、この章では電子の状態密度、Blochの定理、そしてエネルギーバンド構造について掘り下げていきましょう。

固体物理学への導入：電子の世界

この章では、固体物理学における電子の状態密度について解説します。

電子のエネルギーと波数ベクトルの関係、すなわち分散関係が重要です。

固体物理】勾配∇で表す状態密度（導出）

公開日:2019/10/06

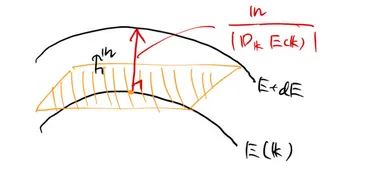
✅ 記事は、3次元自由電子の状態密度と、自由電子でない場合の一般的な状態密度の導出について解説しています。状態密度はエネルギーと波数の関係（分散関係）を用いて求められ、等エネルギー面と勾配の概念が重要となります。

✅ 自由電子の場合との違いとして、エネルギーと波数の関係が異なり、フェルミ面が球形ではなくなる点を挙げています。状態密度は、等エネルギー面で囲まれる領域の体積を計算し、1つの状態が占める体積で割ることで求められます。

✅ 勾配の逆数が等エネルギー面間の距離に、状態密度にどのように関係するかを説明しています。最終的に、状態密度は勾配の大きさの逆数を用いて表され、これが状態密度の計算に不可欠な要素となります。

さらに読む ⇒固体物理・量子力学を中心に｜ばたぱら出典/画像元: https://batapara.com/archives/density-of-states-nabla-gradient.html/

状態密度は、電子のエネルギー分布を理解する上で不可欠ですね。

自由電子の場合との違いも興味深いです。

固体物理学は、物質中の電子の状態に焦点を当て、そのエネルギーを区別することで様々な現象を理解しようとする学問です。

電子は波としての性質を持つため、そのエネルギーは波数ベクトルの関数として表現されます。

この関係性は分散関係と呼ばれ、固体物理学において非常に重要な役割を果たします。

本稿では、なぜ電子に着目し、エネルギーで状態を区別し、エネルギーを波数ベクトルで記述するのか、そして分散関係がなぜ重要なのかを解説します。

えー、状態密度とかむっちゃ難しそうやけど、ま、頑張ってついていこーっと！

Blochの定理：周期的なポテンシャル下の電子の振る舞い

次の章では、Blochの定理について詳しく見ていきます。

周期的なポテンシャル下での電子の振る舞いを理解する上で重要な概念です。

ブロッホ定理（Bloch゛s theorem）のわかりやすい解説 １（ついに出た！）

公開日:2023/01/04

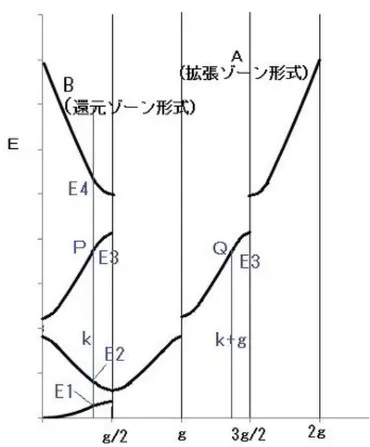
✅ この記事は、周期ポテンシャルを持つ結晶中の波動関数を表すブロッホ定理について、質問サイトの回答を基に分かりやすく解説しています。

✅ ブロッホ定理の証明のステップを、フーリエ変換やシュレディンガー方程式を用いて説明し、専門的な内容を理解しやすくしています。

✅ 記事は、ブロッホ関数、ブリュアンゾーン、還元ゾーン形式など、固体物理学で難解とされる概念についての理解を深めることを目指しています。

さらに読む ⇒SonofSamlawのブログ出典/画像元: https://sonofsamlaw.hatenablog.com/entry/2023/01/04/204520

Blochの定理は、電子が結晶格子内を移動する際の振る舞いを理解するための基礎となりますね。

電子が結晶格子内を移動する際、周期的なポテンシャルの影響を受けます。

この状況下での電子の振る舞いを記述するのがBlochの定理です。

Blochの定理は、電子が結晶内でどのように振る舞うかを理解するための重要なツールであり、特にBloch波の形成に焦点を当てています。

この定理を用いることで、電子の状態を理解するための数理的アプローチを確立できます。

いやー、難しかことばっかりで、俺にはちょっとハードル高いっすねー！でも、なんとなく分かった気になってきたけん、良しとしよう！