波って何?周波数から波動力学まで!波の基礎と応用を徹底解説?波の基礎概念:周波数、波長、波数
光、電波、音…身の回りの「波」を徹底解説!周波数、波長、波数といった基本概念から、電磁波の多様な性質、光の応用まで網羅。電子の波動性や、固体物理学における波の役割も。波の世界をマスターして、科学への理解を深めよう!
波数の数学的表現と変換
光の振る舞いを理解する鍵!波数って何?
光の周波数、波長、エネルギーを表す概念!
3つ目の章では、波数の数学的な表現と、光や電磁波のエネルギー計算について解説します。
数式を用いて、より深く理解を深めましょう。
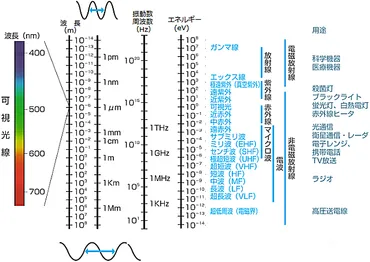
✅ この記事は、光のエネルギーに関する計算方法を解説しており、専門知識がない人にも理解できるよう基礎から説明しています。
✅ 光のエネルギーの計算に必要な公式や単位(ジュール、電子ボルト)を紹介し、波長、振動数、エネルギー間の相互変換の計算式を提示しています。
✅ 可視光線における波長、エネルギー、振動数の関係を表で示し、計算フォームへの波長入力によるエネルギー計算の利便性についても触れています。
さらに読む ⇒光と色と出典/画像元: https://optica.cocolog-nifty.com/blog/2012/01/post-0dfa.html波のエネルギー計算は、少し複雑ですが、理解すると面白いと思います。
数式を追うことで、波の奥深さを感じていただければ幸いです。
波数の概念を理解することは、光や電磁波の振る舞いを理解する上で非常に重要です。
分光学における波数(overline{u})は、光子エネルギー、周波数、波長を表すために用いられます。
光子エネルギーEは、光の振動数(u)とプランク定数hを用いて、(E = hu)と表されます。
光速c、周波数(u)、波長(lambda)の間には、(c = ulambda)の関係があります。
これらの関係から、波数(overline{u})と光子エネルギーEの関係は(E=choverline{u})と表されます。
例えば、波数(overline{u} = 2 times 10^4 cm^{-1})の場合、波長(lambda)は(500 nm)と計算され、周波数(u)は約(6.0 times 10^{14} Hz)となります。
また、この波数に対応する光子エネルギーEは(E=choverline{u})を用いて計算できます。
振動現象を扱う場合は角波数kを用い、これは平面波の進行方向を示す波数ベクトル$bm{k}$と密接に関連します。
波数ベクトルは$f(bm{r},t) = cos(bm{k} cdot bm{r} - omega t)$のように表され、波動方程式における重要な要素となります。
あらまあ!数式がいっぱい出てきて、まるで魔法の呪文みたいじゃね!でもね、光ってエネルギー持ってるんでしょ? なんか不思議ねえ… あたしゃ、わからんわ!
波動力学と波動方程式
量子力学、電子の運動を支配する方程式とは?
波動関数で記述し、波動性と粒子性を持つ。
4章では波動力学と波動方程式について解説します。
量子力学の基礎となる考え方を、分かりやすく説明していきます。
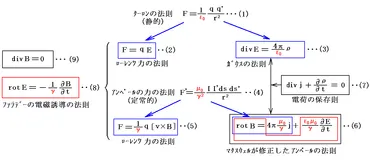
✅ 記事では、様々なPパターンの特性と、それらがどのように関連しているかを解説しています。特定のパターンでは、0または2の値が見られること、また、これらのパターンがどのような状況で現れるかについても言及されています。
✅ 記事では、Pパターンの理論的な側面だけでなく、実際の現象との関連性についても触れられています。例えば、磁場の理論や、特定の科学者の名前を挙げながら、Pパターンの研究がどのように進められてきたかを紹介しています。
✅ 記事は、様々なPパターンの具体的な例と、それらが持つ意味について説明しています。また、特定の条件下でパターンがどのように変化するのか、そして、それらの変化がどのような影響をもたらすのかについても考察しています。
さらに読む ⇒em̍Z(ʖڎ)出典/画像元: http://fnorio.com/0211heterogeneous_wave_equation_2/heterogeneous_wave_equation_2.html波動力学と波動方程式は、少し難しいですが、量子力学の根幹をなす考え方です。
丁寧に解説していきますので、ご安心ください。
量子力学では、電子の波動性と粒子性の二重性に基づき、電子の運動を波動方程式で記述します。
波動力学(シュレーディンガー流)と行列力学(ハイゼンベルグ流)があり、両者は等価であることが知られています。
波動を表す関数として、速度$v$で移動する関数$f(x-vt)$や、位相速度$v$で伝播する正弦波$f(xt) = cos(k(x - vt))$などが用いられます。
平面波は$f(bm{r},t) = cos(bm{k} cdot bm{r} - omega t)$と表され、波数ベクトル$bm{k}$によってその進行方向が決定されます。
電磁波の場合、平面波$bm{E}(bm{r},t) = bm{E}_0 cos(bm{k} cdot bm{r} - omega t)$がマクスウェル方程式から導かれる電磁波の波動方程式$abla^2 bm{E}(bm{r},t) = frac{1c^2} frac{partial^2partial t^2} bm{E}(bm{r},t)$を満たします。
この波動方程式は、$k$と$omega$の間に特定の関係を要求し、波の速度$c$、周期$T$、波長$lambda$の関係$lambda = cT$を示します。
えー、波動力学ってなに?なんか難しそう…。でも、分かんないなりにも、ちょっと興味出てきたかも!勉強って、大事やね!
固体物理学における電子の状態と分散関係
固体物理学で重要な電子の゛顔゛は?
エネルギーと波数ベクトルの関係!
最後の章では、固体物理学における電子の状態と分散関係について解説します。
電子がどのように振る舞うのかを見ていきましょう。
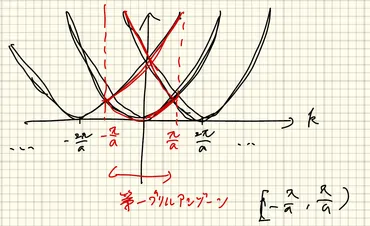
✅ 2原子分子の例を通して、原子が近づくと波動関数が重なり、分子軌道が生成され、バンドギャップが生じることを説明しています。原子の結合力はバンドギャップの大きさに対応します。
✅ 周期的なポテンシャルを持つ結晶中の電子の波動関数はブロッホ関数で表され、結晶の周期性を反映した周期関数と平面波の積の形になります。kは逆格子空間に属し、第一ブリルアンゾーン内で考えることができます。
✅ エネルギーバンドは逆格子の周期性を持ち、k=nπ/aの時にブラッグ反射条件によりバンドギャップが生じます。この現象は、電子が波として振る舞う際に干渉が起こり、エネルギーが不連続になることによります。
さらに読む ⇒物性物理学1』§3:周期ポテンシャル中の「波」としての電子 ...出典/画像元: https://note.com/yukishiomi/n/nbd01f2535d37電子の状態と分散関係は、物質の性質を理解する上で非常に重要です。
丁寧に解説していきますので、最後までお付き合いください。
固体物理学では、電子の状態に焦点を当て、そのエネルギーと波数ベクトルとの関係性、つまり分散関係を重視します。
電子の状態をエネルギーで区別し、そのエネルギーを波数ベクトルで表現することが重要です。
この考え方は、電子が波としての性質を持つことに起因します。
この分散関係を理解することにより、電子の振る舞いを詳細に知ることができます。
固体物理学では、電子の状態をエネルギーで区別し、そのエネルギーを波数ベクトルで表現することで、物質の様々な性質を理解することができます。
いやー、電子とか、まじでミクロな世界の話やん!でも、そーゆーのが、色んな物質の性質に関わってるとか、なんかロマンあるね!俺も、もっと勉強しよっかなー!
今回の記事では、波の基礎から応用までを幅広く解説しました。
皆様、いかがでしたでしょうか。
波の世界は奥深いですね。
💡 周波数、波長、波数といった基本的な概念を理解することで、波の理解が深まります。
💡 電磁波と光の性質、波長と応用について学ぶことで、光の多様な利用法や性質を理解できます。
💡 波数の数学的表現と計算方法を理解することで、より深いレベルでの波の理解が可能になります。