ガチャ確率の謎を徹底解説!?コンプガチャの闇!

💡 ガチャの確率を計算する上で、2項分布やポアソン分布の知識が役に立つ。これらの分布を利用することで、当選確率が低い場合の近似計算を行うことができます。
💡 コンプガチャでは、確率ではなく分散に注目することで当選の可能性が高まる。分散とは確率のばらつきの度合いを表す指標で、分散が大きいほど当選確率が高くなります。
💡 コンプガチャでコンプまでに必要な回数は、景品の種類数に大きく影響される。景品の種類数が増えるほど、必要な回数の期待値も大きくなります。
それでは、本題であるガチャに関する知識を深めていきましょう。
ガチャの仕組みを理解することで、より戦略的にガチャを引くことができます。
ガチャの確率計算方法
ガチャ確率の計算方法には様々な方法があり、当選確率が低い場合には2項分布やポアソン分布を活用します。
コンプガチャを計算する場合には、各アイテムが重複しない確率とコンプガチャを完了するために必要なアイテムの数を考慮します。
また、期待値や確率分布を利用することで、確率を導き出すことができます。

✅ 当選確率が低いガチャ確率を計算する場合、2項分布またはポアソン分布を用いて近似計算することができます。2項分布は特定回数だけ当たる確率を計算するために使用され、ポアソン分布は発生確率がまれで試行回数が非常に多い場合に特定回数だけ当たる確率を近似するために使用されます。
✅ コンプガチャの計算では、必要なガチャの回数の期待値を求めることに加えて、特定の確率でコンプガチャを完了するために必要な試行回数を計算する方法があります。この計算では、各アイテムが重複しない確率と、コンプガチャを完了するために必要なアイテムの数を考慮します。
✅ コンプガチャでは、期待値から確率を計算すると誤差が生じる可能性があります。これは、期待値が平均的な結果を表すためで、実際の結果は期待値と異なる場合があります。そのため、コンプガチャを完了するために必要な試行回数をより正確に計算するには、引く回数を指定して確率を計算する必要があります。
さらに読む ⇒dskjal出典/画像元: https://dskjal.com/statistics/the-probability-of-gacha.htmlガチャ確率の計算は複雑ですが、期待値や確率分布を利用することで確率を導き出すことが可能です。
これらの計算方法を理解することで、ガチャを引く際の戦略を立てることができます。
ガチャの確率計算には、以下の方法があります。
当選確率が低い場合の近似計算:2項分布やポアソン分布を用います。
コンプガチャの計算:コンプに必要な回数の期待値を求めます。
また、具体的確率の求め方も解説されています。
当選確率1%のガチャを100回引いたとき、1回以上当たる確率、当選確率2%のガチャを100回引いたとき、2回以上当たる確率、当選確率1%、天井100回のガチャを250回引いたとき、5枚以上当たる確率、当選確率2%のガチャを99%の確率で手に入れるために必要な試行回数などです。
ははは、確かに難しいっちゃけど、理解できたらガチャを引くのがもっと楽しくなるばい!
コンプガチャでコンプリートに必要な回数
コンプガチャで全ての景品を揃えるのに必要な回数は、景品の種類数と調和級数の積で表されます。
調和級数は発散級数であるため、景品の種類数が増えるほど期待値も大きくなります。
そのため、コンプガチャの期待値は、景品の種類数が増えるほど指数関数的に増加します。

✅ コンプガチャで全ての景品を揃えるのに必要な回数の期待値は、景品の種類数(n)に調和級数(1 + 1/2 + 1/3 + ... + 1/n)をかけたもので表されます。調和級数は発散級数であるため、景品の種類数が増えるほど期待値も大きくなります。例えば、10種類の景品を集めるには平均して約23回、100種類の景品を集めるには平均して約460回のガチャを引く必要があります。
✅ コンプガチャの期待値の計算方法は、期待値の線形性を利用する方法と、期待値の漸化式を立てる方法があります。期待値の線形性を利用する方法では、期待値を各景品を揃えるために必要な回数の期待値の和として計算します。期待値の漸化式を立てる方法では、ある段階で持っている景品の種類数からコンプするまでに必要な回数の期待値を計算し、漸化式を解くことで全体の期待値を求めます。
✅ コンプガチャの期待値はおよそ景品種類の数の対数倍となります。これは、調和級数がnが大きいときにlog(n) + γに漸近するためです(γはオイラー定数)。したがって、景品の種類が多くなると、コンプするために必要なガチャの回数も指数関数的に増加します。
さらに読む ⇒学びTimes | 学びを、もっと、面白く。出典/画像元: https://manabitimes.jp/math/1053コンプガチャの期待値は、景品の種類数が増えるほど指数関数的に増加します。
そのため、コンプするのに必要なガチャの回数は景品の種類数に大きく依存します。
景品の種類数が多いコンプガチャでは、期待値よりも多くのガチャを引く必要があることを覚えておきましょう。
コンプガチャで全ての景品を揃えるのに必要な回数の期待値は、「景品の種類数(n)」×「1からnまでの調和級数(1+1/2+1/3+…+1/n)」で表されます。
これは、各景品が等確率で出現すると仮定した場合の値です。
景品の種類数が多いほど、コンプに必要な回数の期待値は大きくなります。
例えば、10種類の景品を集めるには約23回、100種類の景品を集めるには約460回のガチャが必要です。
ふふふ、コンプするまでには根気が必要よ。運も味方につけるといいわね。
ガチャの確率分布計算方法
ガチャで当選するには「分散に期待する」ことが重要で、確率よりも分散の幅に注目することで当選確率が高まります。
分散が大きいほど当選確率が高くなるため、たとえ今回当選しなくても、分散の力で次回以降で当選する可能性が高まります。
公開日:2023/08/23

✅ ガチャはリアル福引とは異なり、ハズレを引いても当選確率は常に一定のため、100回引いても当選しない確率は約4割と、直感的な確率よりも当選しにくい仕組みになっています。
✅ ガチャで当選するには「分散に期待する」ことが重要で、確率よりも分散の幅に注目することで当選確率が高まります。たとえ今回当選しなくても、分散の力で次回以降で当選する可能性が高まるため、モチベーションを維持してガチャを引き続けることが大切です。
✅ 実際のガチャの実験では、当選確率0.87%のキャラを80回で引き当て、確率よりも分散の力を活用することが証明されました。この実験では、80回引いて少なくとも1回当選する確率は約47%でしたが、分散の力により、確率よりも早く当選することができました。
さらに読む ⇒アイオイクスの社員ブログ出典/画像元: https://clm.seojapan.com/2992ガチャの実験では、分散の力により確率よりも早く当選することが証明されました。
分散を味方につけることで、ガチャをより戦略的に引くことができます。
ガチャの確率分布を計算するには、ガチャの内容、抽選回数、重複排除の有無を考慮します。
ガチャの内容とは、各アイテムの当選確率です。
抽選回数とは、ガチャを引く回数です。
重複排除とは、同じアイテムが複数回当選したときに、その後の抽選で当選確率が0になることを意味します。
これらの要素を考慮して、各アイテムの当選確率を計算し、抽選回数で割ります。
重複排除を行う場合、重複アイテムの確率は0にします。
計算した確率を合計して確率分布を作成します。
この確率分布は各アイテムの出現確率を表します。
へぇー、確率より分散の方が大事なんや!
ガチャに関するプレイヤーの状況
ランク54に到達し、恒常ガチャで入手できるキャラクターをほぼ完凸させ、キャラクターを全員コンプリートしている。
総戦力は80,000以上、キャラランクの合計は520となっており、相当やり込んでいることが窺える。
このプレイヤーは、ゲームを極めようとしていることが伺えます。
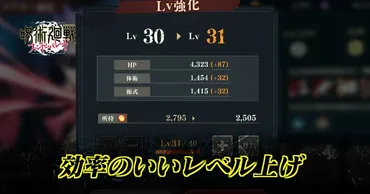
✅ プレイヤーはランク54に到達しており、恒常ガチャで入手できるキャラクターをほぼ完凸(限界突破)させている。また、キャラクターを全員コンプリートしている。
✅ 総戦力は80,000以上、キャラランクの合計は520となっており、相当やり込んでいることが窺える。
✅ この情報は、呪術廻戦ファントムパレードの攻略記事の一部であり、プレイヤーの状況やゲームの進捗状況を把握するためのデータとして提示されている。
さらに読む ⇒ゲームエイト出典/画像元: https://game8.jp/jujutsuphanpara/578070このプレイヤーは相当なやり込みプレイヤーであることが分かります。
ゲームを心から楽しんでいるのでしょう。
プレイヤーはランク54で、恒常ガチャキャラをほぼ完凸、キャラクターをフルコンプ済み、総戦力は80,000以上、キャラランク合計は520です。
これは、かなりやり込んでいるプレイヤーであることがわかります。
さすがやねぇ、これならどんな敵も楽勝やろ!
その他
ガチャからアイテムを入手する確率が一定の場合、必要な回数の期待値は nH(n) となり、ここで n は景品の種類数、H(n) は調和数である。
調和級数は発散級数であるため、景品の種類数が増えるほど期待値も大きくなります。

✅ コンプガチャに必要な回数の期待値は、期待値の線形性と幾何分布に従うという事実を使用して計算できる。ガチャからアイテムを入手する確率が一定の場合、必要な回数の期待値は nH(n) となり、ここで n は景品の種類数、H(n) は調和数である。
✅ 景品の種類数が多いコンプガチャでは、コンプまでに必要な回数が期待値よりも多くなる傾向がある。これは、新しいアイテムを入手する確率が低くなるためである。
✅ コンプガチャの数学モデルは、ゲームデザイナーやセールス担当者が予測可能な結果をもたらすゲームを設計したり、売上目標を達成するための戦略を立てたりするのに役立てることができる。
さらに読む ⇒doryokujin゛s blog出典/画像元: https://doryokujin.hatenablog.jp/entry/2012/05/09/034209コンプガチャの数学モデルは、ゲームデザイナーやセールス担当者が予測可能な結果をもたらすゲームを設計したり、売上目標を達成するための戦略を立てたりするのに役立てることができます。
このモデルを活用することで、より戦略的なガチャシステムを構築することができます。
期待値の線形性や漸化式を用いてコンプガチャに必要な回数の期待値の計算式を証明できます。
また、コンプガチャでは、景品の種類数が多いほど、実際の確率は期待値よりも低くなることに注意しましょう。
あら、あなた数学がお好きなの?頭が良くていらっしゃるのね。
本日はガチャに関する知識を深めていただきました。
ガチャを引く際には、確率だけでなく、分散や期待値についても考慮することで、より戦略的にガチャを引くことができます。
ガチャの仕組みを理解することで、より賢く、より楽しくガチャを引きましょう。
💡 ガチャ確率を理解することで、コンプガチャに必要な回数の期待値を計算したり、当選確率を高める戦略を立てたりすることができる。ガチャの仕組みを理解した上でプレイすることで、より戦略的にガチャを引くことができます。
💡 コンプガチャでは、景品の種類数が多いほど、期待値よりも多くのガチャを引く必要がある。コンプガチャをプレイする際は、景品の種類数と期待値を考慮することが重要です。
💡 ガチャの実験では、分散の力により、確率よりも早く当選することが証明されている。分散を味方につけることで、ガチャをより戦略的に引くことができます。